中学１年生が図形の解き方で、新しい公式を見つけた！と報告してくれました。

名付けてバームクーヘン面積（笑）

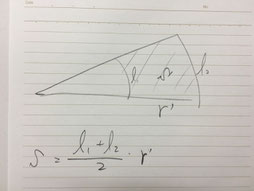
右図のバームクーヘンを切ったような形の面積Sを求めるのに、通常は、大きな扇形ー小さな扇形で求めますが、その生徒の解法はバームクーヘンを台形に見立てて、

S=（内側の弧＋外側の弧）/２×（半径の差）
になる！って教えてくれました。

ちなみに、学校の数学の先生に話をしたけど、合ってるかよくわからない・・・ってウヤムヤにされたそうです（笑）

そこで、彼の新発見が正しいか、頑張って証明してみました！

通常どおり大きな扇形ー小さな扇形で求める式から変形していくと、左図のように、
S=（内側の弧＋外側の弧）/２×（半径の差）
となり、無事証明できました。

最初は、積分を使って証明していたのですが、途中で、もっと簡単に証明できそうって気づいて、因数分解の和と差の公式を利用して（つまり中学3年までのレベルの知識で）求めることができました。

式の変形問題として、中3に出してみよっかな（笑）

もしかして、上記の式は、裏ワザとかで教えている塾があるのかもしれませんが、（そんなにバームクーヘンの面積を求める問題は出ませんね（笑））少なくとも私には初めての考え方だったので、とっても新鮮でしたね！

そして、そんな斬新な発想ができる生徒を思いっきり称えてあげました！
ホント素晴らしい発想力です！

ちょうどお父さんがお迎えに来られたので、上記を説明し、この発想の豊かさがいつまでも続くようにしていきたいですねと、意見が一致しました。