１週間のお休みを頂き、今日から、夏期講習の後半がスタートしました！

あいにくの天気と、お盆休みでお出かけするご家族も多く中学生が少なく、逆に課題が多くて苦しんでいる高校生が、頑張って夏休みの課題を進めていましたね。

そんな高校生の一人から、数学の課題について相談を受けました。

テーマは自分で決めていいので、数学に関して、レポートを書くようにというものです。

あまりに自由すぎて、テーマが浮かばないとのことだったので、こちらの思考実験の本から、こんなのどう？とテーマをアドバイスしてみました。

この中の、確率の有名な問題で、「モンティ・ホール問題」というのが掲載されています。

アメリカのバラエティ番組で、わずか３つの扉から１つを選ぶというとっても単純な問題にも関わらず、当時は学者も含めて大論争に発展したそうです。

番組の内容はこうです。

A、B、C　3つのドアがあります。

プレイヤーはこのうち1つの扉を選択し、それによって景品をもらうというゲームです。

3つのドアのうちの1つのドアの先には豪華な車があり、このドアを選択すれば車を手にすることができます。

残りの2つの扉はハズレで、いずれもヤギが配置されています。

車=アタリ、ヤギ=ハズレ、という単純な選択ゲームです。

ただし途中、司会者のモンティ・ホールが、ある駆け引きを持ち掛けます。

駆け引きでプレーイヤーを据さぶる、それがこのゲームの見どころというわけです。

では、やってみましょう。

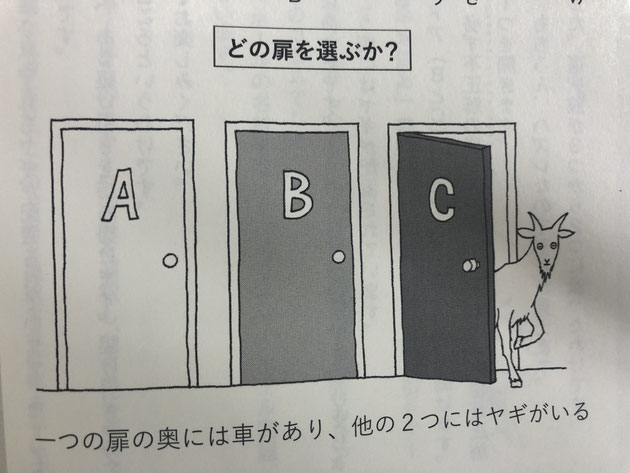
プレイヤーはあなたです。3つのうち1つのドアを選びましょう。1つの扉には車が、他の2つの扉の向こう側にはヤギが配置されています。

仮にあなたはAの扉を選んだとします。次に、モンティは演出として残りの2つのドア（BとC）のうち1つを選んで扉を開けます。このとき、モンティは正解を知っており、必ず不正解の扉を開きます。

もし、Aの扉が正解の場合、不正解の2つの扉からランダムに1つを開きます。仮に今回はCの扉を開いたとしましょう。もちろん、ハズレなのでヤギが見えます。

これで、車があるドアはAかBとなりました。選択肢が3つから2つに減ったわけです。

そして、モンティはあなたに語り掛けます。

「選ぶ扉を変えてもいいですよ」

今ならBの扉に選択を変えることができるというのです。

さて、選ぶ扉を変えたほうがいいのでしょうか？

思考を巡らせてみてください。

Cがヤギとわかったので、残る扉はAとB

Aの扉とBの扉、どちらを選択したほうが車を当てる可能性が高まるのでしょうか。

あるいは確率は同じでしょうか。

それなら最初の選択のままでいいような気もします。

多くの方は、残りのドアが２つになったことで、「確率は1/2か・・・ならば、直感を信じて、選んだドアを変えないほうがいいな。」と考えるそうです。

しかし、数学的に確率を計算すると、変えたほうが、変えない方の２倍！当たる確率が増えます！

２倍に増えるって、びっくりしますよね。

高校生も、まったく信じられない！とのことだったので、実験をしてもらいました。

３つのコップの中に１つだけ当たりを入れ、生徒に当ててもらいます。

最初にこれ！と言って決めたコップ以外の２つのうち、ハズレの方のコップを開けた上で、選び直してもらうのですが、今回は必ず変更してもらいました。

そして、必ず変更してもらった上で当たったかどうかを、50回繰り返してもらい、その数を集計したところ・・・

当たった回数・・・32回

ハズレた回数・・・18回

となりました。

今回は必ず変更してもらっているので、もし全部変更しなければ、逆の回数となっていたので、変更しなければ18回しか当たらなかったことになります。

つまり、変更しなければ当たりが18回だったものが、変更したので、32回に増えたということが言えます。

32/18＝1.78　倍と、変更することで約2倍近く当たる確率が上がったとこが実験からもわかりますね。

実は、この「モンティ・ホール問題」そっくりな問題が、昨年の日進中学２年の定期テストに出題されています。

（２）の予想後に、入っていない箱を伝えた上で、AとCを選び直しができる場合の確率って、上記のモンティ・ホール問題で、ヤギのいる扉を一つ開けた後、「選ぶ扉を変えることができますよ」と、言われて迷っている状況と同じです。

昨年、この試験では、ほとんどの生徒が、（ア）、（イ）とも１/２と答え、正解者はいなかったと聞いています。

正解は、こちらのブログの記事から確認してみてくださいね（笑）

生徒には、正解のブログの記事を読んでもらいましたが、それでも、どうしても納得できないと困っていました。

ホント、正直な生徒です（笑）

なので、ムリに、わかったふりはしなくてもいいよと言って、レポートには、そのまま実験結果と、説明を読んでみたけどわからないことを素直に書いてもらっています。

そもそも、モンティ・ホール問題が、「直感で正しいと思える解答と、論理的に正しい解答が異なる問題」の適例とされているぐらい、モヤモヤする問題なので、仕方が無いとは思います。

レポートを読んだ先生が、納得できる説明をしてくれるといいんですけどね。

正解の記事を読んだ皆さんは、納得できましたか？

進路選びに役立つ先月の人気記事TOP5です！

小中学生のお父さん・お母さんにも知ってほしい、子どもの進路について考えよう！

高校生の通知表は、最低、平均3.5以上をめざそう！

私立高校実質無償化！？　実際は年収による制限が

通知表を見て怒らないで下さいね。

2020年の大学入試、一発勝負の戦いを挑むか、日々の努力で合格を勝ち取るか。